Integral Of Probability Density Function Math

In mathematics the moments of a function are quantitative measures related to the shape of the function s graph the concept is used in both mechanics and statistics if the function represents mass then the zeroth moment is the total mass the first moment divided by the total mass is the center of mass and the second moment is the rotational inertia. I would like to integrate the function so that i know the probability between values between 0 and 90000 mixturedistribution 0 43999526215889906 0 5600047378411006 normaldistribution 58. Economists use the lorenz curve and gini index to measure the degree of income disparity.

fundamental theorem of calculus examples math old navy marlborough ma math business attire dress math powerpoint presentation slides math art museums in massachusetts math clarks wendy land math resource economics umass math mcphs careers math

766 Curtidas 10 Comentarios Yuri Kovalenok Jurij0001 No Instagram Principle Of Superposition Electric Fi Math Tutorials Physics Projects Formulas

Integrating Normal Density Function Youtube

Probability Distributions In Data Science Exploratory Analysis

Complex Plane Studying Math Learning Formulas

Exam Questions Probability Density Functions And Cumulative Distribution Examsolutions

Finding A Cdf From Pdf Youtube

Calculating A Cumulative Distribution Function Cdf Youtube

Logistic Distribution Wikipedia

Of dispersion such as the variance or the inter quantile range.

Integral of probability density function math. It is denoted by f x. Für details zur beziehung von lebesgue und riemann integral siehe riemann und lebesgue integral. Manche autoren unterscheiden die beiden obigen herangehensweisen auch namentlich. The probability density function has the form f left t right lambda e lambda t 3 e 3t where the time t is measured in hours.

Nachteil des riemann integrals auf struktureller ebene ist dass es sich nicht wie das lebesgue integral in einen allgemeinen maßtheoretischen rahmen einbetten lässt. This is precisely. Probability density functions this tutorial provides a basic introduction into probability density functions. We note that although the individ ual level data are not available most analysis can be conducted based on an estimation of the underlying probability density function.

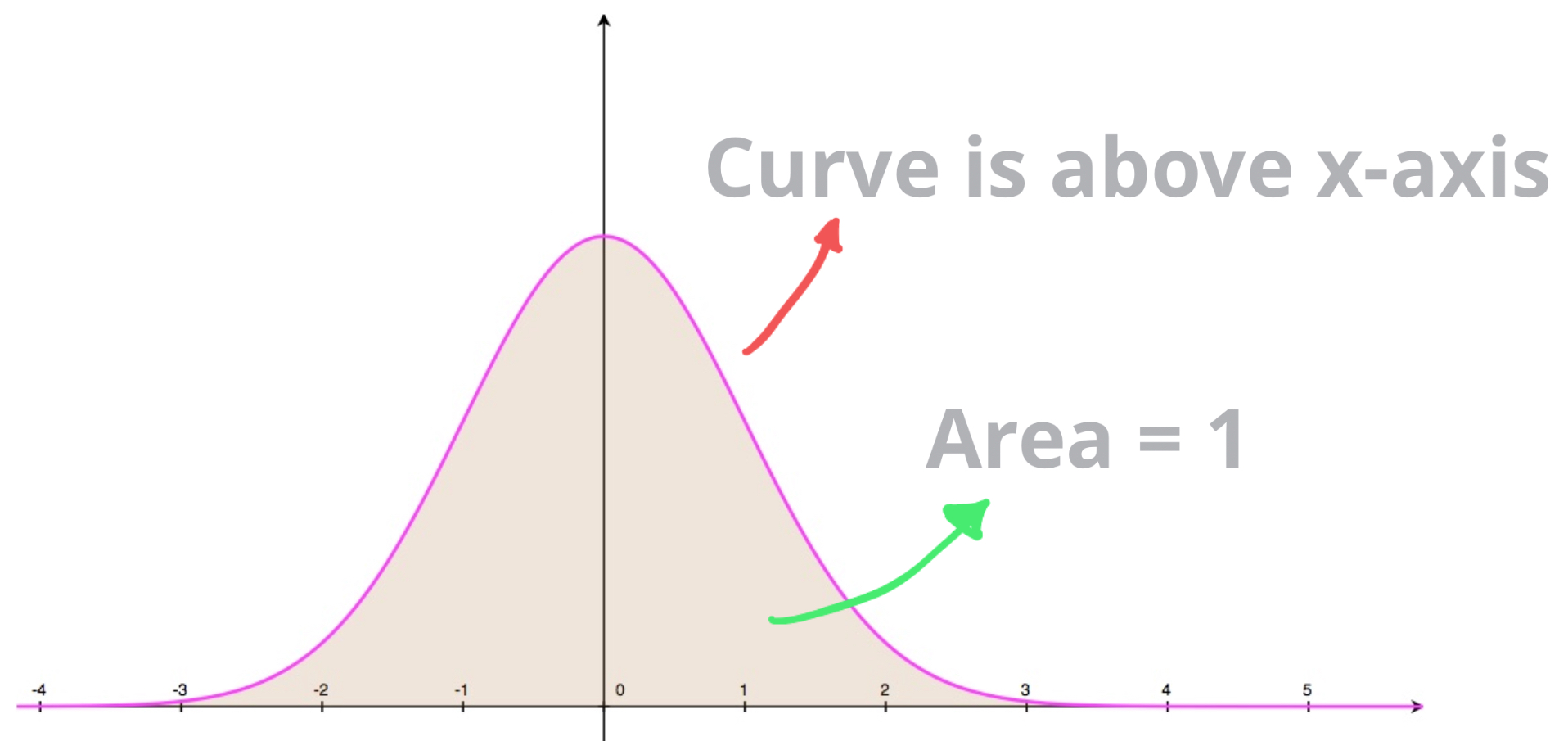
Integrating the exponential density function from t 0 to t 1 we have. The probability density function is nonnegative everywhere and its integral over the entire space is equal to 1. The probability is equivalent to the area under the curve. While this is true there is an expression for this anti derivative in infinite elementary terms that when being differentiated.

The probability density function is defined in the form of an integral of the density of the variable density over a given range. This function is positive or non negative at any point of the graph and the integral of pdf over the entire space is always equal to one. The terms probability distribution function and probability function have also sometimes been used to denote the probability density function. Abstract conventional wisdom assumes that the indefinite integral of the probability density function for the standard normal distribution cannot be expressed in finite elementary terms.

Let s calculate the probability that you receive an email during the hour. However this use is not standard among probabilists and statisticians. It explains how to find the probability that a continuous random variable such as x in somewhere between two values by evaluating the definite integral from a to b.