Eigenvalue Meaning Math

The eigenvalue tells whether the special vector x is stretched or shrunk or reversed or left unchanged when it is multiplied by a. The eigenvalue problem is a problem of considerable theoretical interest and wide ranging application. The german prefix eigen roughly translates to self or own.

are fish herbivores math angle that measures 180 degrees math w2 example math kristina hong math environmental resume math iodine nuclear fallout math u of i unofficial math goddard definition math

The Eigenvalue Power Method Example 1 Linear Algebra Problems Youtube

Pdf Eigenvalues And Eigenvectors Embodied Symbolic Formal Thinking

Solving Linear Systems With Eigenvalue Eigenvector Method Example 2 Youtube

Http Www Math Usm Edu Lambers Mat461 Spr10 Lecture17 Pdf

Pdf Application Of Power Method And Dominant Eigenvector Eigenvalue Concept For Approximate Eigenspace Solutions To Mechanical Engineering Algebraic Systems

Pdf Student Thinking About Eigenvalues And Eigenvectors Formal Symbolic Embodied Notions

Pdf The Eigenvalue Problem For 1 Biharmonic Operator

Https Arxiv Org Pdf 1711 01301

If av λ v for v a 0 we say that λ is the eigenvalue for v and that v is an eigenvector for λ.

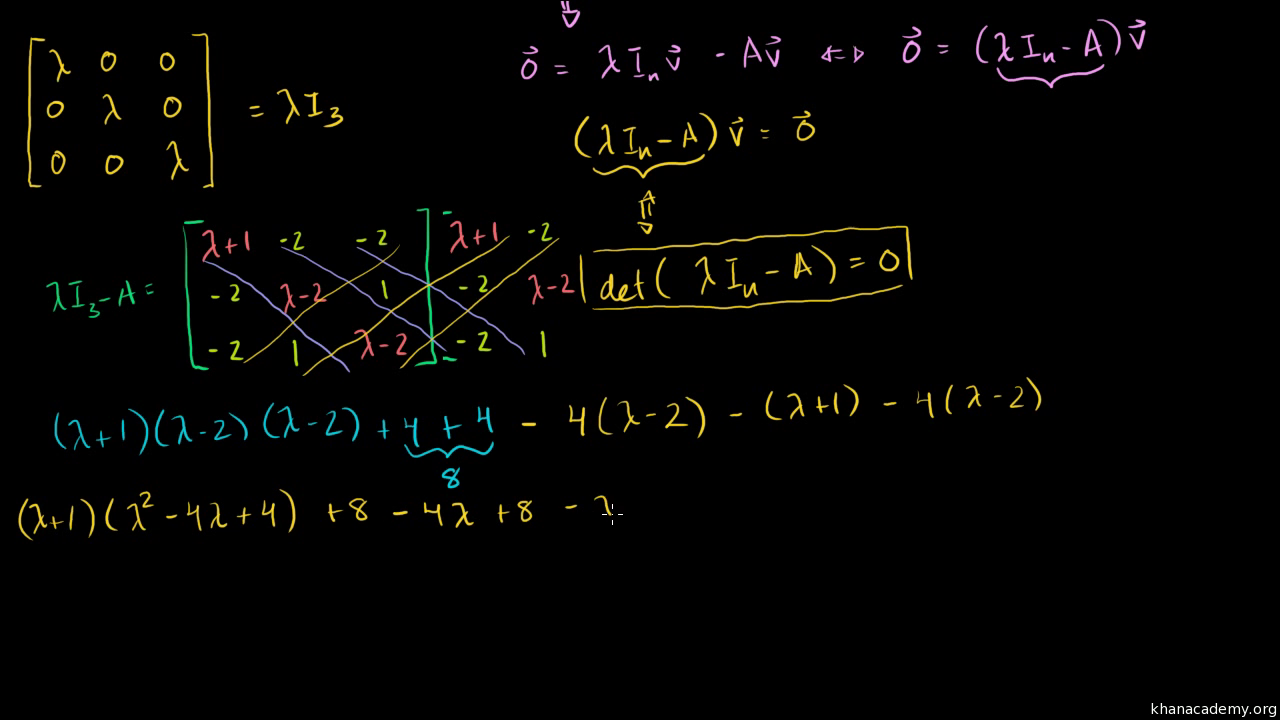
Eigenvalue meaning math. The eigenvector of a matrix is also known as a latent vector proper vector or characteristic vector. Eigenvalue definition is a scalar associated with a given linear transformation of a vector space and having the property that there is some nonzero vector which when multiplied by the scalar is equal to the vector obtained by letting the transformation operate on the vector. Eigenvectors are also useful in solving differential equations and many other applications related. The basic equation isax d x.

The number is an eigenvalueofa. For example this problem is crucial in solving systems of differential equations analyzing population growth models and calculating powers of matrices in order to define the exponential matrix. The eigenvector is a vector that is associated with a set of linear equations. If t is a linear transformation from a vector space v over a field f into itself and v is a nonzero vector in v then v is an eigenvector of t if t v is a scalar multiple of v this can be written as where λ is a scalar in f known as the eigenvalue characteristic value or characteristic root associated with v.

And the eigenvalue is the scale of the stretch. The solutions to this equation may also be subject to boundary conditions that limit the. These special eigenvalues and their corresponding eigenvectors are frequently used when applying linear algebra to other areas of. 1 means no change 2 means doubling in length 1 means pointing backwards along the eigenvalue s direction.

Every square matrix has special values called eigenvalues. Other areas such as physics sociology biology economics and statistics have focused considerable attention on eigenvalues and eigenvectors their applications and their computations. Multiply an eigenvector by a and the vector ax is a number times the original x. A root of the characteristic equation of a matrix.

An eigenvalue of a is a scalar λ such that the equation av λ v has a nontrivial solution. There is a direct correspondence between n by n square. These are defined in the reference of a square matrix. In mathematics an eigenfunction of a linear operator d defined on some function space is any non zero function f in that space that when acted upon by d is only multiplied by some scaling factor called an eigenvalue as an equation this condition can be written as for some scalar eigenvalue λ.

There are also many applications in physics etc.